
Cos goes opposite from sine, and tangent and cotangent are derived from them so you can always calculate them easily. This lesson may look a bit complicated to remember, but it really is not. Consider Sine, Cosine, Tangent, and Cotangent: Following table is very important to remember. The unit circle shown on the applet below. Special angles are angles that have relatively simple values. However, values of sine, cosine and tangent are defined for angles between negative infinity and positive infinity. In one quarter of a circle is $\frac.$$ Trigonometric functions of special angles If you have your number line marked with radians, this is how it would look:įirst, you have a usual unit circle. That means that infinitely many points from number line will fall into same places on a unit circle. In some point you’ll start your second lap around it, and when you wrap it again, you’ll start third and so on in infinity. You wrap an endless line around a circle. Now that we remembered that, let’s look at our picture. One whole circle has $ 2 \pi$ radians one half of a circle has $\pi$ radians and so on. 1 radian is a part of a circle where length of an arc is equal to the radius. The positive numbers, (up from the origin in the picture) are replicated in a positive mathematical orientation (counterclockwise) and negative (downwards from the origin) are replicated in a negative mathematical orientation (clockwise). It is important that the radius of this circle is equal to 1.Īs you know, you have positive and negative numbers on your number line. The unit circle is a circle with a radius of 1. For every point on our number line, there is exactly one point on a circle. Now what would happen if we would wrap our endless line around a circle with radius 1?Įvery point from the number line will end up on our circle. A number line is a straight endless line with origin and unitary length. The reference number is t' = π/3, which determines the terminal point (1 /2, √3 /2) from the table shown above.īecause the terminal point determined by t is in quadrant III, its both x-coordinate and y-coordinate are negative.Before learning about what a unit circle is, it helps to remember what is a number line. The reference numbers associated with these values of t were found in Example 11. The reference number is t' = π/4, which determines the terminal point ( √2/2, √2 /2) from the table shown above.īecause the terminal point is in quadrant IV, its x-coordinate is positive and its y-coordinate is negative. After years of seeing other teachers share pictures of the unit circle projects their students created, I decided to finally take the plunge. The reference numbers associated with these values of t were found in Example 10. 9 More Activities for Teaching Trigonometry. For example, the segment from E to F is a diameter of.
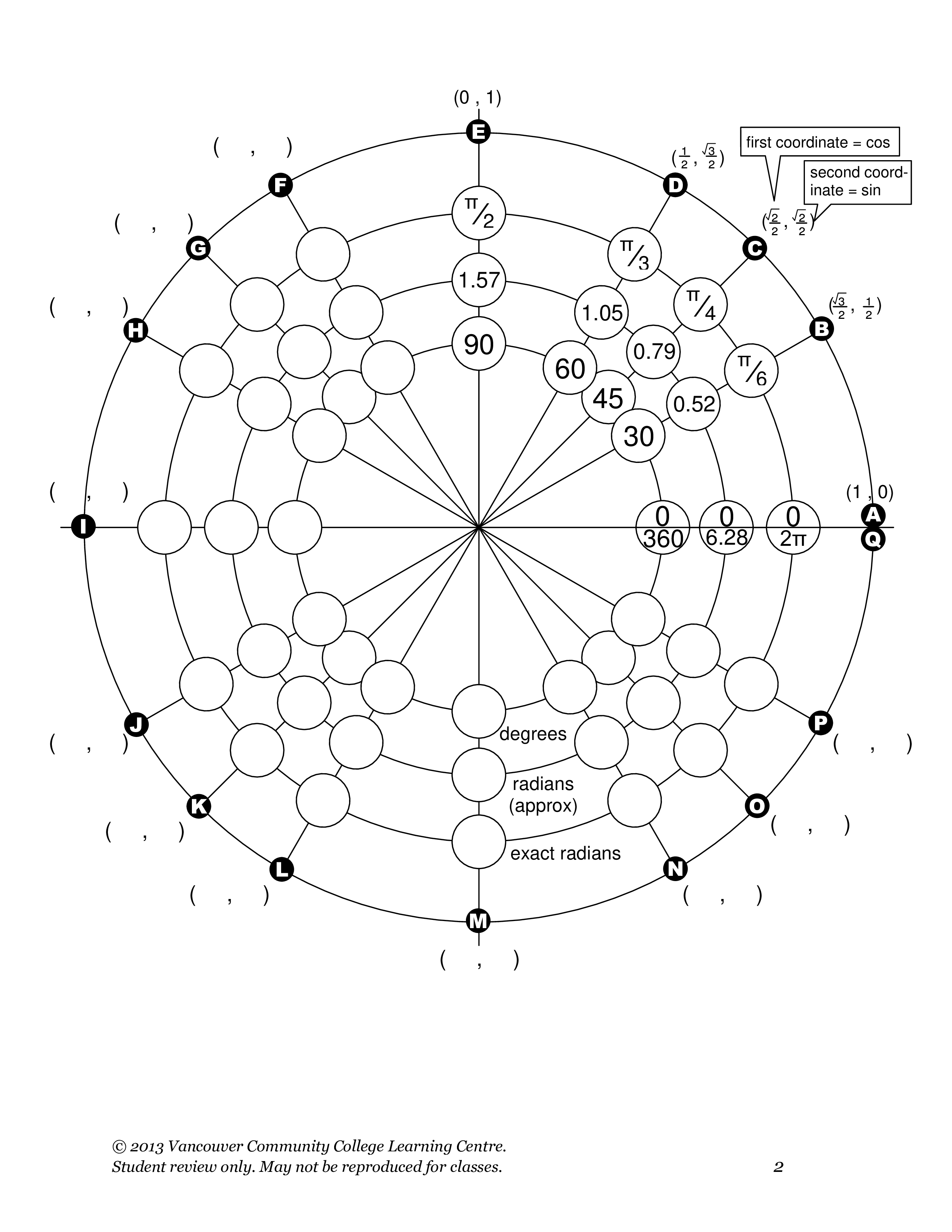
The line segment between two points on the circle and through the center is called the diameter. This week your student will learn why circles are different from other shapes, such as triangles and squares. The reference number is t' = π/6, which determines the terminal point ( √3/2, 1 /2) from the table shown above.īecause the terminal point determined by t is in quadrant II, its x-coordinate is negative and its y-coordinate is positive. Unit 3 Big Ideas Circumference of a Circle. Moreover, the second-degree equation with two variables x and y is used to represent the unit circle algebraically. However, the cartesian coordinate plane is commonly used to depict the unit circle. The reference numbers associated with these values of t were found in Example 9. A unit circle is defined as a circle with a radius of one unit. The terminal point determined by t is P( ±a, ±b), where the signs are chosen according to the quadrant in which this terminal point lies.įind the terminal point determined by each given real number t. Find the terminal point Q(a, b) determined by t'.ģ. To find the terminal point P determined by any value of t, you we can use the following steps :Ģ.


 0 kommentar(er)
0 kommentar(er)
